Marker frontpladen. Universal skala.
Del 1. Hvorfor "universel" skala?
Jeg havde et behov for at opdele et rundt emne i 7 dele. Jeg prøvede at dele 360 med 7. Så hvad? Ikke delt sporløst! Og straks spørgsmålet: hvordan kan skalaen på frontpladen, markeret i 360 dele, hjælpe mig? opdeling efter en grad? Svar: ingen måde.
Derfor kom ideen til at markere frontpladen med anvendelse af en universel skala på den. Tanken er at sætte yderligere 4 skalaer på hovedskalaen.
Hovedskalaen, lad os kalde det, er frontplades layout på 15 grader. På frontpladen mærker vi "0", "90", "180" og "270". Derefter på begge sider af hvert af mærkerne risikerer vi forskellige divisionsværdier. Så på en sektor fra 330 til 30 grader ("0" eller "360" i midten) vil vi placere en skala på 60 divisioner, dvs. en division vil være lig med 6 grader.
I en sektor mellem 60 og 120 grader ("90" i midten) skal du placere en skala på 48 opdelinger, dvs. en division vil være lig med 7,5 grader.
I frontpladesektoren mellem 150 og 210 grader ("180" i midten) markerer vi skalaen med 42 divisioner, det vil sige prisen for en division er 8,75 grader.
I frontpladesektoren mellem 240 og 300 grader ("270" i midten) placerer vi en skala på 36 opdelinger, dvs. med en opdelingspris på 10 grader.
Og nu er der få argumenter til fordel for en sådan fordeling af frontpladen.
1. Ved hjælp af skalaen "42" kan vi opdele cirklen i 7 dele, fordi 42 er divideret med 7 uden en rest - dette er 6 opdelinger. Derfor kan du med sin hjælp opdele cirklen i 14, 21, 42 dele. En skala på 360 dele tillader ikke dette.
2. Når vi fordeler frontpladen i 360 opdelinger, kan vi opdele i 2, 3,4,5,6,8,9,10,12,15, 18,20,24,30,36,40,45,60,90,120,180 opdelinger og kun 21 værdier.
Den universelle skala ud over disse værdier gør det muligt at nedbryde flere flere værdier: 7, 14, 16, 21, 48, 72, 80, 144, 240. Det vil sige mindst 30 værdier.
Følgelig er den universelle skala mere funktionel end 360-divisionsskalaen.
Del 2. Lidt om teorien om fejl.
Vi må acceptere for aksiomen, at enhver (!!!) måling vi kun kan gøre med en fejl. Ellers er det praktisk taget umuligt at udføre nogen måling uden fejl.
Målenøjagtighed påvirkes af flere faktorer. Vi viser nogle af dem.
1. Ethvert måleværktøj er forskelligt fra referencen.
2. Ethvert slag har reelle lineære dimensioner.For eksempel har spidsen af en kompasnål en "tykkelse" på adskillige mikron, for eksempel 10. Når vi kombinerer en lineal med et sådant slag, kan vi ikke "ved øje" bestemme, hvilken del af stryget kanten af linealen falder på: en, anden eller tredje mikron tykkelse.
3. Den mest skærpede blyant har også en tykkelse på ca. 0,2 mm. Desuden ændres denne tykkelse med hvert slag på grund af slid af grafit.
Konklusion: til praktiske behov i hjem betingelser, kan vi "stole" på nøjagtighed inden for et par hundrededele af en millimeter.
Baseret på ovenstående betragtninger skal de skarpeste nåle, flade linealer, pæne hænder og et skarpt øje anvendes ved markering af frontpladen.
Del 3. Markup.
Til mærkning lavede jeg en ramme fra stænger, et stykke fiberplade. Rammen blev fastgjort til maskinen med klemmer, mens skærmens plan (fiberplade med et ark papir) skulle være vinkelret på maskinens føringer. Og endnu et krav: skærmen skal placeres ikke kun vinkelret, men også således, at linealen, der er monteret på en akse i maskinens chuck, glider hen over skærmen uden et hul. Dette arrangement er nødvendigt for størst mulig eliminering af markeringsfejl.
Vær opmærksom på det faktum, at vores provisoriske lineal af zinkbelagt trim også passer tæt på frontpladen, og den "arbejdsdel" (den del, som vi trækker ud risici), skal være vinkelret på frontpladen. I stedet for at beskære galvanisering, kan du naturligvis tage en metal lineal. Men trimmen kan let bøjes for at passe tæt på frontpladen. Sikret med en belastning. Jeg har denne metalskive.
Linjen fra hjørnet har fem huller, alle placeret på den samme linje. Et hul med en diameter på 5,8 mm. En 6 mm hårnåle indsættes i den, som fastgøres med møtrikker på begge sider. De følgende 4 huller borede jeg med en 1 mm bor, og de er placeret fra aksen for henholdsvis det første hul 195 (for 36 divisioner), 220 (for 60), 241 (for 42), 260 (for 48 divisioner) mm. Af erfaring vil jeg sige, at boret skal tages dobbelt så tyndere - 0,4 - 0,5 mm. Men jeg havde ikke det ved hånden. Faktum er, at vi vil indsætte en skærpet blyant i disse huller, og ved at dreje linealen, vil vi tegne buer med den tilsvarende radius. Spidsen af en blyant i et hul med en diameter på 1 mm hænger lidt, dvs. radius tegnes med en lille fejl - 2-3 snesevis.
Linealen "løsner" på bæreren, når den ydre møtrik løsnes. Jeg har dette stykke bord tændt under min arm. Men måske bare en skrue.
Lidt geometri.
Alle de ovenfor nævnte præparater er nødvendige for dette. Der er et sådant begreb inden for geometri - en ligesidet trekant. Dette er en geometrisk figur, der har lige sider, og følgelig lige vinkler imellem dem, det vil sige 60 grader. I vores tilfælde vil vinkelens toppunkt være maskinens spindelakse, "materialiseret" i form af en fastklemt 6 mm hårnåle, hvorpå en lineal fra et aluminiumshjørne er fastgjort. Trekanten ligger derfor på sin side. Vi tegner dens base på skærmen i form af en akkord mellem seriffer på den tilsvarende bue.
Hvordan gør man det?
Ved hjælp af en skærpet blyant og det andet, tredje, fjerde og femte hul i den svækkede lineal tegner vi på et arkpapirark.
Mål derefter 260 mm fra det nederste punkt på den ydre bue, og få det andet (øverste) punkt på basen i den ligesidige trekant.
Hvorfor på den ydre bue? Det er muligt på en hvilken som helst af dem, men jo større radius, desto mere nøjagtigt kan vi markere og tegne et akkord - trekantens base. Faktisk er det ikke nødvendigt at tegne en basislinje: vi vil kun bruge seriffer på kurven, som er vertikaterne i trekantens sidevinkler - vinklerne ved dens base.
Vi kan bruge denne egenskab ved en ligesidet trekant som følger: vores lineal fra et hjørne, sænket ned til en understøtning, er på linje med et punkt på trekantens base. Derefter fastgør vi linealen med nøglen og stram møtrikken. Vi risikerer på frontpladen, skriver det første mærke på "scotch tape" - "O". Drej patronen med hånden, indtil linealen er på linje med det andet punkt på trekanten.
Således blev frontpladen drejet 60 grader. Vi mærker på frontpladen med en nål, og på bånd skriver vi, at det er "60".
Derefter svækkes møtrikken, der sikrer linealen, linealen går ned, "til basen", uden at røre ved patronen. Det vil sige, linealen er igen på linje med det første punkt i basen af trekanten. Spænd møtrikken, fratager linealen mobilitet. Drej chucken med hånden, indtil linealen er på linje med det andet (øverste) punkt på trekanten. Vi risikerer på frontpladen, skriver på bånd, at det er "120". Og så videre, ved hjælp af den samme algoritme, markér frontpladen med etiketterne "180", "240" og "300".
Som et resultat får vi muligheden for at opdele cirklen i 2, 3 og 6 dele.
Gå videre. Vi er nødt til at få risiciene på frontpladen med en opdeling på 30 grader. For at gøre dette skal basen af trekanten opdeles i halvdelen. Som et resultat vil linealens rotationsvinkel fra bundpunktet til et nyt punkt i midten af basen være 30 grader. Der er to måder at dele basen på en trekant på. Første. Vi tager en lineal, og fra bundens nederste punkt udsætter vi 130 mm, det vil sige halvdelen af basens længde (akkorder).
Den anden er geometrisk. Vi tager et kompas, og med dets hjælp, når vi har spredt benene i en længde, der er mere end halvdelen af basens længde (i mit eksempel ca. 150-160 mm), strejker vi på den ene og den anden side af basen, der overlapper den foreslåede sektor med halvdelen af basens længde. Derefter arrangerer vi kompasnålen øverst i trekanten uden at ændre afstanden mellem kompassbenene og gøre de samme risici, som bør overlappe hinanden med de tidligere trukkede. Vi forbinder de resulterende punkter, og i skæringspunktet mellem denne linje og basislinjen i trekanten vil være halvdelen af længden af denne base.
Og nu bruger vi den samme algoritme, vi deler frontpladen og forårsager opdelinger gennem 30 grader. For at gøre dette skal du kombinere et af de tidligere anvendte mønstre med kanten af den øverste lineal. Væk møtrikken, sænk linealen til bundpunktet. Vi fastgør møtrikken, drej drejebænken til et nyt mærke på 30 grader. Vi risikerer at skrive den tilhørende etiket på skotbåndet. For eksempel, hvis risikoen for "120" blev kombineret, får vi et mærke på 150 grader ved at dreje patronen i en retning med uret. Og hvis du drejer det mod uret, får du 90 grader. Og så videre for alle tidligere modtagne risici (mærker), indtil frontpladen er helt fyldt med mærker med opdelinger på 30 grader.
Som et resultat får vi muligheden for at opdele cirklen i flere værdier: i 4, 8 og 12 dele.
Nu, for at afslutte anvendelsen af divisionerne i hovedskalaen, skal du anvende divisionen til en pris på 15 grader. Det vil sige, sektorer på 30 grader skal halveres på nogen måde. Vi har allerede gennemgået dette, i den forstand, at vi gjorde det for sektorer på 60 grader. Så vi får mærker på skærmen med en opdeling på 15 grader, og med deres hjælp lægger vi risici på frontpladen.
Så hovedskalaen er klar, det vil sige en skala med opdelinger til en pris af 15 grader.
Nu skal du anvende yderligere 4 skalaer på denne hovedskala for at opdele i 60, 48, 42 og 36 divisioner. Grafisk ser det sådan ud:
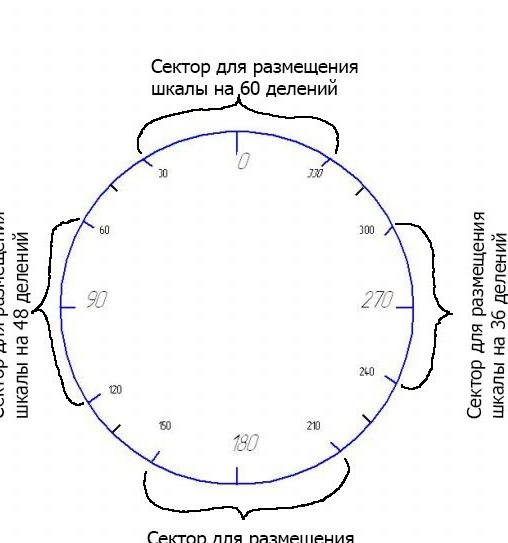
Jeg placerede vægterne i den rækkefølge. Men du kan placere en hvilken som helst af disse skalaer ethvert andet sted efter din skøn. Jeg fandt denne placering mere praktisk. Bemærk, at mellem skalaerne forblev intakte sektorer på 30 grader. Du kan selvfølgelig udvide sektorens sektorer på grund af de resterende frie sektorer. Jeg gjorde ikke dette for ikke at overbelaste vægten. For eksempel, for en skala fra 42 divisioner, vil 5 hak ved 8,57 med risiko for 180 i en hvilken som helst retning blive "forsvaret" med 42,85 grader. Det vil sige næsten tæt på markeringerne 135 eller 245, hvilket kan komplicere brugen af dem.
Del 4. Tegning af en skala fra 60 divisioner.
For at nedbryde denne skala, er vi nødt til at få divisioner med en pris på 6 grader. For at gøre dette igen en lille geometri. For at få en trekant i en cirkel med en vinkel på spidsen af 6 grader, er vi nødt til at beregne længden på bunden af en sådan trekant. Trekanten vil være ensidig, og basen af den trekant, der er indskrevet i en cirkel, er en akkord.
Formlen til beregning af akkorden er: L = 2 * R * sin (A / 2), L er længden på akkorden, R er cirkelens radius, A er vinklen.
Af alle de kendte mængder ved vi kun værdien på vinklen - 6 grader. At finde en halv sinus fra 6 grader er et spørgsmål om teknologi.
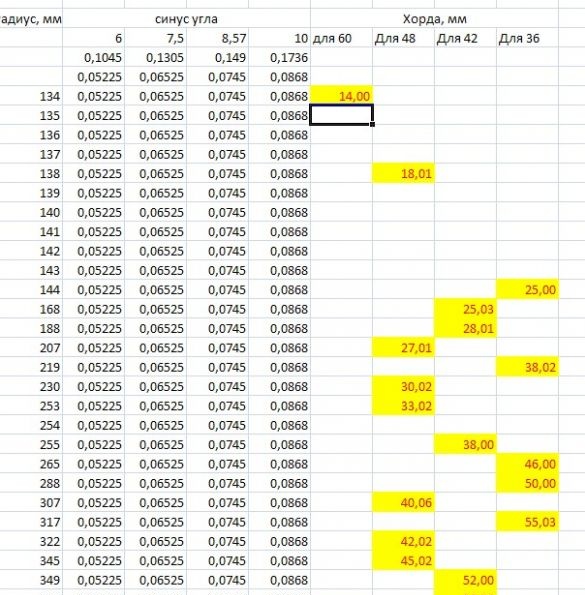
Det gjorde jeg senere: Jeg brugte metoden "videnskabelig poke". Ved hjælp af Excel-programmet, en tabel, hvor jeg inkluderede længder af radier med graduering gennem 1 mm, startende fra 130. Og ifølge formlen fik jeg værdierne for akkordlængderne. Tabellen viste sig at være lang, en del af denne tabel efter sletning af unødvendige værdier (fraktioneret) så sådan ud:
Det gjenstår at vælge de ønskede værdier. Da beregningerne blev foretaget nøjagtige til 0,00001, valgte jeg for det første endda værdier, der kan deles med 4. For det andet de, der kunne afrundes, hvis der ikke var mere end 0,03 efter decimalpunktet. Dette er spørgsmålet om fejl: vi kan ikke "spore" tre hundrededele, når vi bruger skalaer. Lad mig minde dig om, at blyantlinjens tykkelse er mindst 0,2 mm. Så hundrededele kan forsømmes forsvarligt (vi er allerede vant til, at der altid er fejl i målingerne).
Hvorfor er det nødvendigt at "dele" med 4? Men enkel. Når alt kommer til alt delte vi først basen af trekanten med 2 og derefter igen med 2. Og som et resultat fik vi et heltal, ikke en brøkdel.
Valget af værdier så sådan ud:
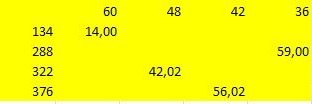
Men så nægtede jeg dette valg, da mellem 134 og 376 mm afstanden er for stor. Og kiggede efter andre betydninger. Fundet det. De er ikke længere i tabellen, fordi Jeg skar dem ud. Disse værdier er 195.220.241 og 260 mm. Buer med sådanne radier er placeret ganske kompakt uden at forstyrre hinanden. Ja, ikke alle kan deles med 4 uden en rest. Og vi har ikke brug for alt. For at oprette hovedskalaen tog jeg buen med den største radius. For at opdele i halvdelen brugte jeg den grafiske metode, dvs. ved hjælp af et kompas. Og hvis du beslutter at bruge en lineal, - et flag i dine hænder! - er en skala med en radius på 260 mm opdelt to gange i halvdelen uden resten. Længderne på akkorderne er henholdsvis 34, 23, 36 og 34 mm.
Så i sektoren for en skala til opdeling i 60 divisioner er vi nødt til at anvende risici med en opdelingspris på 6 grader. Hvordan gør man det? Alt er enkelt som et bip fra en damplokomotiv. Ved hjælp af en lineal eller kompas udsætter vi et 23 mm akkord fra et lavere eller ethvert andet punkt på en bue med en radius på 220 mm. Risikoen på frontpladen med en værdi af "90" er kombineret med kanten af den øverste lineal. Vi kombinerer den nederste lineal med den ene ende af det opnåede akkord, fastgør møtrikken, klemmer linjalen. Vi drejer patronen for at justere linjens kant efter akkordens anden ende. Fik en vinkel på 6 grader. Med en kompasnål risikerer vi risikoen på frontpladen. For at fremskynde processen (og reducere antallet af målefejl i det mindste lidt) er det bedre at bruge kompasset til at fremstille seriffer ikke for en akkord, men for flere. Så er det ikke nødvendigt at løsne møtrikken hver gang for at justere linealen med bundpunktet, men simpelthen efter anvendelse af de næste risici drejer vi patronen, indtil den næste risiko (slutningen af den næste akkord).
Del 5. De resterende skalaer.
Længden på akkorden for en skala fra 36 divisioner er 34 mm, som vi som før markerer på buen, men med en radius på 195 mm. Hvis du "fremstiller" 6 sådanne akkorder, kan du begynde at markere skalaen med værdien "240" og afslutte med værdien "300". Prisen for en division er 10 grader.
Og endvidere er skalaen ifølge den velprøvede algoritme ved hjælp af en 260 mm bue opdelt i 48 opdelinger (længden af akkorden er 34 mm). Opdelingsprisen er 7,5 grader.
Ved hjælp af en bue på 241 mm er skalaen opdelt i 42 opdelinger. Akkordlængden er 36 mm, opdelingsprisen er 8,57 grader.
Konklusion.
Endnu en gang om spørgsmålet: hvorfor har dette brug for at komplicere markeringen så meget? Svaret er enkelt: har ikke brug for dig, ikke. Jeg havde brug for sådan en sammenbrud for at fremstille tandhjul med tænder til 42 og 48 tænder i fremtiden. Brug stadig skalaer til 29 og 32 tænder. Men jeg vil gøre dem allerede tilgængelige ved hjælp af en midlertidig opdeling af bånd. Men det vil være senere.
Og det sidste spørgsmål: hvordan man bruger det, fordi hver af skalaerne (undtagen den vigtigste) er kort, er hele segmentet 1/6 af frontpladsens omkreds?
Svar: let at bruge. Jeg viser lidt senere videoen (når jeg monterer den). I mellemtiden fortæl kort.
Du skal sætte bånd på patronen. I stedet for en skal du tage de to øverste linealer. Det er bedre fra galvanisering, så linealen let kan bøjes.
Og nu et par eksempler. Lad os sige, at vi er nødt til at markere en cirkel i 6 dele. For at gøre dette skal du bruge hovedskalaen med en øverste lineal. Ved konsekvent at kombinere risikoen for 0, 60, 120, 180, 240 og 300 får vi en opdeling i 6 dele. Cirklen, men spis, men er fastklemt i patronen, som vi roterer og tager risici langs kanten af skæret eller ved selve skæret.
Marker nu cirklen, der er fastgjort i patronen, i 5 dele. Der er ingen sådanne opdelinger på hovedskalaen.Lad os så tænke, hvilken af skalaerne der kan deles med 5 uden resten? Sandt: 60 bar skala. Dette er 12 divisioner. Men forbandet: vi har kun 10 divisioner i skalaen !?
Rolig uden panik. Prisen for en opdeling af denne skala er 6 grader. Derfor er 12 opdelinger 72 grader. Og på hovedskalaen i det forrige eksempel brugte vi sektorer på 60 grader. Og hvad forhindrer os i at kombinere den ene øverste linje med risikoen for "300", og den anden linje til at kombinere på den anden risiko til venstre for "0". Det vil sige, tilføj 60 gange 2 gange til 6, vi får 72. Vi placerer linealerne, så de passer tæt på frontpladen. Arbejder ikke Det er sandt, at frontpladsens radius er for lille, krumningen er stor, og linealerne hænger enten i luften, eller de bliver nødt til at blive bøjet kraftigt, så de passer tæt på frontpladen. Gør hverken det ene eller det andet. Bare tænd for hovedet, og i stedet for 12 divisioner, lad os tage 6 divisioner, dvs. 36 grader. Og vi bliver herskere gennem 6 divisioner.
På bånd med en blyant eller pen vil vi tegne bindestreger på linealerne. På vores cirkel laver vi det første hak med en skær. Vi drejer patronen med hånden, lad os sige i løbet af uret, indtil det venstre slag på klæbebåndet er rettet mod kanten af den højre lineal. Vi vendte 36 grader. På bånd på venstre lineal trækker vi en risiko og vender patronen til denne risiko. Så vi vendte os 72 grader. Vi laver et andet hak med et skær. Og så videre. Én subtilitet. Streber med en pen eller blyant er "tykke", uanset hvor hårdt du prøver. Derfor skal kanten af den højre lineal, når du roterer patronen, ikke kombineres med højre kant af venstre linje, men med dens venstre kant. Det vil sige, at næsten fuldstændigt linjen skulle gå under den rigtige lineal. Ellers akkumuleres en fejl på 2-3 dusin med hver måling. Og i en cirkel kan det være mere end en millimeter.
For at opdele i 14 dele skal du bruge en skala fra 42 divisioner. 42: 14 = 3 opdelinger.
Mere interessant er spørgsmålet om sammenbrud, antag at for 144 dele. Jeg ved ikke, hvem der har brug for det, men pludselig? Her er algoritmen anderledes. Vi har ikke skalaer, der kan deles med dette antal. Derefter leder vi ikke efter antallet af hak med grader af en opdeling. 360: 144 = 2,5 grader. Hvor får man 2,5 grader? Og hvis på vores skala? !! Vi har en skala med en opdelingspris på 10 grader. Og der er en skala med en opdelingspris på 7,5 grader. Hvis 10 - 7,5 = 2,5. Her er det ønskede resultat! Hvordan får man det til? Skalaen 36 bringes til toppen, til linealerne. Vi kombinerer en lineal med en risiko for skalaen, en anden med en anden og den nærmeste. Mellem herskerne har vi en sektor på 10 grader. Nu drejer vi patronen og bringer skalaen til 48 til linealerne. Prisen for dens opdelinger er 7,5 grader. Vi kombinerer en risiko for skalaen, for eksempel med den venstre lineal, som vi ikke rørte ved. Derefter flytter vi denne lineal til den anden, indtil den er på linje med den nærmeste risiko for skalaen med 48. Det vil sige, vi reducerer sektoren på 10 grader med 7,5. I resten mellem herskerne får vi en 2,5 graders sektor. Og gå! Ved det samme princip som ved opdeling i 5 dele bruger vi to linealer.
Okay, et andet eksempel. Antag, at du vil bryde en cirkel i 40 dele. Tælles: 360: 40 = 9 grader. Græd - vi har ikke sådan en skala! Tænd på hovedet. Vi har en skala med en opdelingspris på 7,5 grader. To afdelinger på denne skala udgør en sektor på 15 grader. Sæt linealerne i afstand fra hinanden i to divisioner i en skala fra 48.
Og nu fra 15 er du nødt til at trække 6 for at få de ønskede 9 grader. Hvor har vi 6? Det er rigtigt, i en skala fra 60. Vi ved allerede, hvordan man skal tage et par grader ved hjælp af herskere. Det gør vi, mærke.
Ved hjælp af det samme princip kan en cirkel opdeles i 80 dele. 360: 80 = 4,5 grader. Tre opdelinger på en skala fra 48 giver 3 x 7,5 = 22,5. Tre opdelinger i en skala fra 60 giver 3 x 6 = 18 grader. 22,5 - 18 = 4,5.
Og igen til fejlteorien. Hvis du cirkler et stort antal mønstre, akkumuleres fejlen ved hvert mærke. For at reducere fejlen anbefaler jeg, at du markerer halvdelen af mærkerne. Og vende derefter tilbage til begyndelsen og gør markeringen i den anden retning, også til det halve. Når disse "halve" markerer konvergerer (og de næsten aldrig konvergerer), vil vi se størrelsen på den akkumulerede fejl. For eksempel, når jeg delte i 8 dele, viste jeg en fejl i markeringen på ca. 0,1 - 0,2 mm. For gevindforbindelser er dette ikke kritisk: gevindene på skruerne fejles altid med 3-4 snes. Men hvis jeg gik med markeringen i rækkefølge, kunne størrelsen af fejlen stige til 0,5 mm, og dette er allerede meget.Konklusionen fra teorien om stort antal: jo mindre målinger vi foretager, jo mindre tager vi fejl. Og omvendt, jo flere målinger, jo mere akkumuleres fejlen. Dette skal tages i betragtning.